引言

“数十年的金融衍生品交易领域沉浮后，小龙终于就快在一家券商做到了金工组的小Boss。这时候大Boss对其进行最后一项考验，要求其设计一个完美的期权产品。这是挑战也是机遇，如何为该期权产品进行合理定价让他感到万分苦恼。请你帮他解决该问题。”

期权，其实是一种权利的交易，期权的买方可以向期权的卖方支付一定的权利金，以获得期权合约赋予的、在合约规定时间，按事先确定的价格（执行价格）向期权卖方买进或卖出一定数量期货合约的权利。在这场交易游戏中，买方拥有的是权利，可以行使或不行使，而卖方（小龙）拥有的则是义务，一旦买方要求行使权利，无论市场是否利好，都必须履行。在这个过程中，无论标的资产在履约时间中变动到什么样的价格，买方的最大损失无非权利金，而卖方则从买方手中获得权利金以弥补其承担的市场风险。

不难看出来，这场期权游戏中，充满着非线性，也让这场交易更加有趣。因此小龙需要合理地对期权进行定价（权利金的价格），才能保证长期来看回报为正。那么有什么有效的定价方法呢，回想我们在小学时学过的二叉树与蒙特卡洛模拟方法，结合BS方程，或许在该问题上提供新的解决思路。

本文第二章给出了所提出模型的摘要，由于小龙没有具体说明选择美式期权还是欧式期权（区分：欧式期权的买方在到期日前不可行使权利，只能在到期日行权。美式期权的买方可以在到期日或之前任一交易日提出执行），本文对两者都进行了讨论；第三章给出了变量名称表；第四章简要介绍定价原理（数学过敏者慎看）；第五章则是模型效果展示。

（注：需要代码的宝子，评论区扣1，免费奉上完整代码）

摘要

本模型基于二叉树、蒙特卡洛模拟法、BS方程，对美式看涨期权(call)、美式看跌期权(put)、欧式看涨期权(Call)、欧式看跌期权(Put)进行了期权定价。这里我们使用了期权定价的二叉树模型和Black-Scholes-Merton定价公式来对期权定价，并使用蒙特卡洛模拟算法来模拟股票价格中的 （服从标准正态分布）的抽样，将得到的期权价值结果与使用二叉树、BSM定价公式得到的结果进行对比，并多次重复实验以减小误差，从而得到蒙特卡洛模拟后的期权价格。

【关键词】蒙特卡洛模拟、期权定价模型、二叉树模型、BSM方程

变量名称

变量名 变量含义 变量单位
T 距离行权日的时间 年
ST T时刻标的资产价格 美元
K 标的资产行权价格 美元
r 无风险利率 %
q 连续股息率 %
μ^\hat\mu 风险中性定价率 %
σ\sigma 股票收益的年化波动率 无量纲
CTC_T 欧式看涨期权在T时刻的价值 美元
PTP_T 欧式看跌期权在T时刻的价值 美元
n 步数 次

定价原理

基于二叉树的期权定价模型

  • 思路

    ​ 假定到期且只有两种可能，而且涨跌幅均为10%的假设都很粗略。

    修改为：

    ​ 在TT分为很多小的时间间隔Δt\Delta t，而在每一个Δt\Delta t，股票价格变化由SS到SuSu或SdSd。如果价格上涨概率为pp，那么下跌的概率 为1−p1-p。

  • u,p,du,p,d的确定

    我们假定市场为风险中性，也就是说股票预期收益率μ\mu等于无风险利率rr。

    这里我们假设：

    ud=1ud = 1

    又有：

    E(St+Δt)=SerΔt=p∙Su+(1−p)∙SdE\left(S_{t+\Delta t}\right)=S e^{r \Delta t}=p \bullet S u+(1-p) \bullet S d

    并且股票的价格符合布朗运动

    ΔS∼N(rSΔt,σ2S2Δt)V(St+Δt)=E(St+Δt2)−E(St+Δt)2\Delta S \sim N\left(r S \Delta t, \sigma^2 S^2 \Delta t\right) \\ V\left(S_{t+\Delta t}\right)=E\left(S_{t+\Delta t}^2\right)-E\left(S_{t+\Delta t}\right)^2

    得：

    σ2S2Δt=p(Su)2+(1−p)(Sd)2−[pSu+(1−p)Sd]2\sigma^2 S^2 \Delta t=p(S u)^2+(1-p)(S d)^2-[p S u+(1-p) S d]^2

    因此我们可以确定p、u、dp、u、d​的值：

    {u=eσΔtd=e−σΔt\begin{cases} u=e^{\sigma \sqrt{\Delta t}}\\ d=e^{-\sigma \sqrt{\Delta t}}\\ \end{cases}

    令a=erΔta=e^{r \Delta t}，得：

    p=a−du−dp=\frac{a-d}{u-d}

    在行权日TT时刻，期权的价格为：

    {CT=max⁡(0,ST−K)PT=max⁡(0,K−ST)\left\{\begin{array}{l} C_T=\max \left(0, S_T-K\right) \\ P_T=\max \left(0, K-S_T\right) \end{array}\right.

    但考虑到折现的因素，在第tt日，期权的价格为距离到期日TT的预期收益折现值（若考虑连续股息率，需将rr替换为r−qr-q）

    {Ct=PV[E(max⁡(0,ST−K))]=e−r(T−t)E(max⁡(0,ST−K))Pt=PV[E(max⁡(0,K−ST))]=e−r(T−t)E(max⁡(0,K−ST))\left\{\begin{array}{l} C_t=P V\left[E\left(\max \left(0, S_T-K\right)\right)\right]=e^{-r(T-t)} E\left(\max \left(0, S_T-K\right)\right) \\ P_t=P V\left[E\left(\max \left(0, K-S_T\right)\right)\right]=e^{-r(T-t)} E\left(\max \left(0, K-S_T\right)\right) \end{array}\right.

基于蒙特卡洛模拟算法的期权定价模型

鉴于美式期权会在执行期到达前行权，因此常使用蒙特卡罗算法来估计欧式期权的价值以及标的资产的到期价格。

使用蒙卡模拟进行期权定价，需要在风险中性环境中

风险中性定价原则认为：

  • 标的资产的预期收益率 = 无风险利率；
  • 从而对未来的现金流进行无风险利率折现；

仅仅是概率空间的变换，没有提到投资者是风险中性的，因此不用对投资者的风险喜好进行假设。

若考虑会有连续股息率为qq，则μ=r−q\mu=r-q。在行权日TT​时刻，期权的价格为：

{CT=max⁡(0,ST−K)PT=max⁡(0,K−ST)\left\{\begin{array}{l} C_T=\max \left(0, S_T-K\right) \\ P_T=\max \left(0, K-S_T\right) \end{array}\right.

但考虑到折现的因素，在第tt日，期权的价格为距离到期日TT的预期收益折现值（若考虑连续股息率，需将rr替换为r−qr-q）

{Ct=PV[E(max⁡(0,ST−K))]=e−r(T−t)E(max⁡(0,ST−K))Pt=PV[E(max⁡(0,K−ST))]=e−r(T−t)E(max⁡(0,K−ST))\left\{\begin{array}{l} C_t=P V\left[E\left(\max \left(0, S_T-K\right)\right)\right]=e^{-r(T-t)} E\left(\max \left(0, S_T-K\right)\right) \\ P_t=P V\left[E\left(\max \left(0, K-S_T\right)\right)\right]=e^{-r(T-t)} E\left(\max \left(0, K-S_T\right)\right) \end{array}\right.

通过伊藤过程和维纳过程：我们得到STST​的公式：

∂G∂St=1St,∂G∂t=0,∂2G∂St2=−1St2d(ln⁡St)=(μ−12σ2)dt+σdztln⁡ST−ln⁡St=(μ−12σ2)(T−t)+σϵT−t\begin{aligned} & \frac{\partial G}{\partial S_t}=\frac{1}{S_t}, \frac{\partial G}{\partial t}=0, \frac{\partial^2 G}{\partial S_t^2}=-\frac{1}{S_t^2} \\ & d\left(\ln S_t\right)=\left(\mu-\frac{1}{2} \sigma^2\right) d t+\sigma d z_t \\ & \ln S_T-\ln S_t=\left(\mu-\frac{1}{2} \sigma^2\right)(T-t)+\sigma \epsilon \sqrt{T-t} \end{aligned}

求得：

S(T)=S(0)exp⁡[(μ^−σ22)T+σεT]S(T)=S(0) \exp \left[\left(\hat{\mu}-\frac{\sigma^2}{2}\right) T+\sigma \varepsilon \sqrt{T}\right]

这里ε\varepsilon是从期望为0，标准差为1.0的正态分布中的抽样，接下来对ε\varepsilon进行蒙特卡罗模拟并代入S(T)S(T)方程中，即可得到结果。

对ε\varepsilon进行1000次蒙特卡罗模拟后得到ε\varepsilon的均值，将该均值作为ε\varepsilon的估计。按照样本的标准差，同时得到期权在TT时刻的价格（欧式看涨期则为CTC_T；欧式看跌期则为PTP_T）

基于BS方程的期权定价模型

我们可以使用下面的方程对欧式期权进行定价分析：

{c=S∗exp⁡(−q∗T)∗N(d1)−K∗exp⁡(−r∗T)∗N(d2)p=K∗exp⁡(−r∗T)∗N(−d2)−S∗exp⁡(−q∗T)∗N(−d1){d1=ln⁡(S/K)+(r+12σ2)TσTd2=d1−σT\begin{aligned} & \left\{\begin{array}{l} c=S * \exp (-q * T) * N\left(d_1\right)-K * \exp (-r * T) * N\left(d_2\right) \\ p=K * \exp (-r * T) * N\left(-d_2\right)-S * \exp (-q * T) * N\left(-d_1\right) \end{array}\right. \\ & \left\{\begin{array}{l} d_1=\frac{\ln (S / K)+\left(r+\frac{1}{2} \sigma^2\right) T}{\sigma \sqrt{T}} \\ d_2=d_1-\sigma \sqrt{T} \end{array}\right. \end{aligned}

使用方法及效果展示

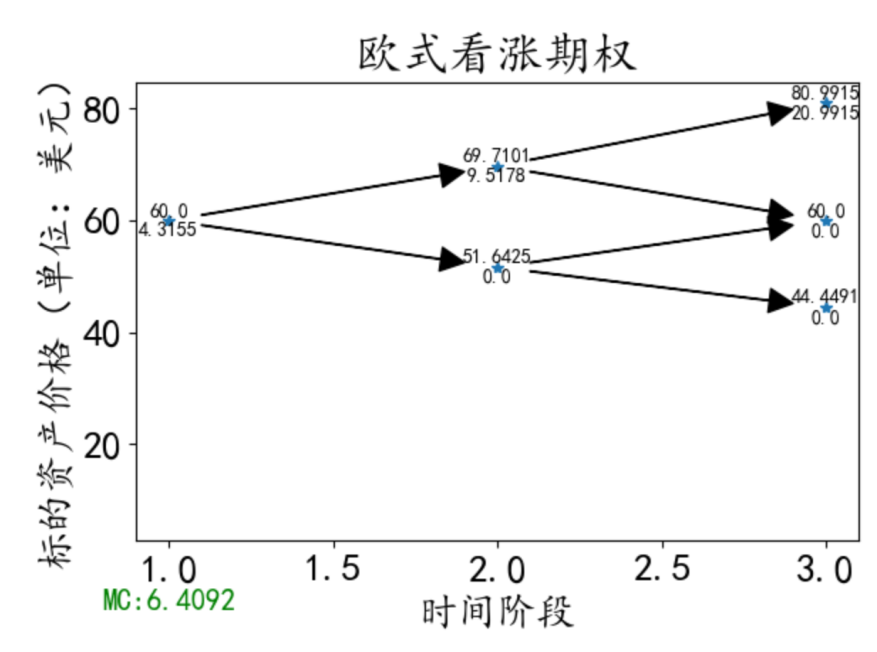
针对S0=50，K=52，r=0.04,q=0.01,T=2,n=2S_0=50，K=52，r=0.04, q=0.01, T=2, n=2的欧美式看涨期权

按照提示数字输入参数

  • 若是欧式期权：

  • 若是美式期权：

得到结果

  • 欧式期权结果：

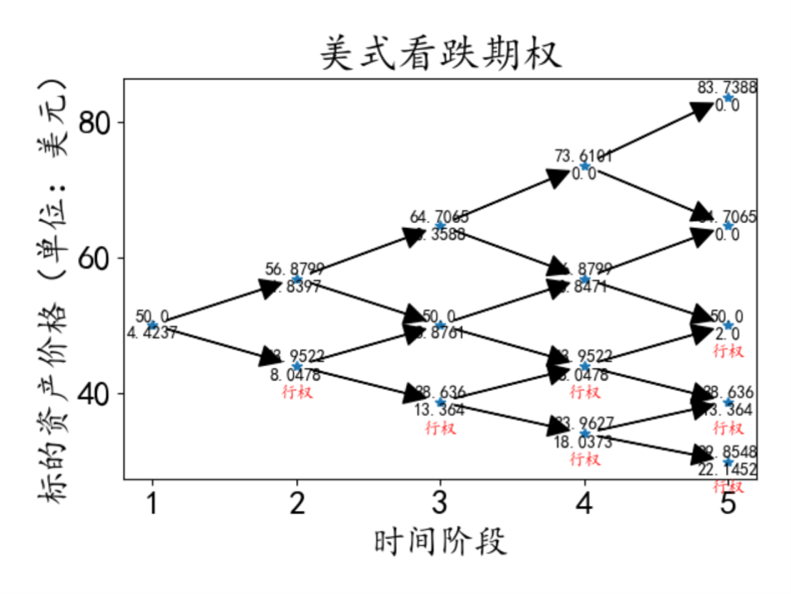
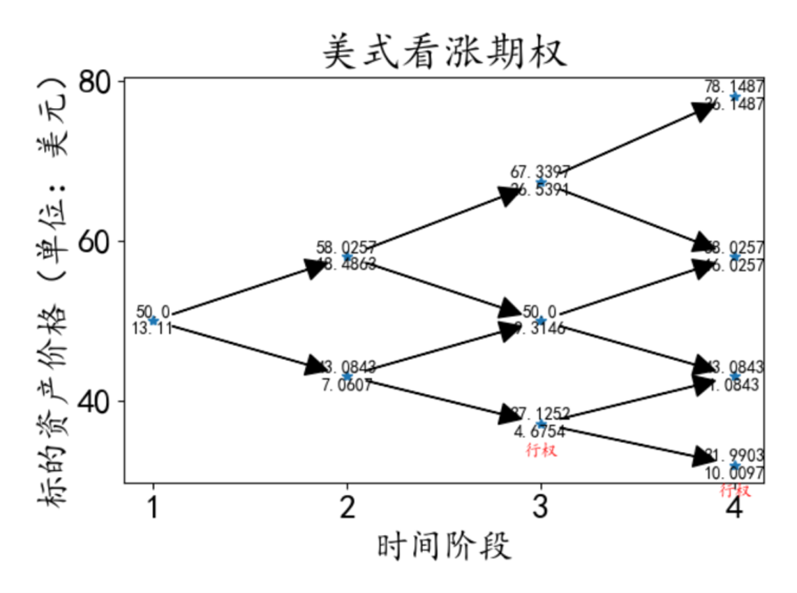
  • 美式期权结果：

二叉树分析

  • 欧式期权：

    注：图中MC为由蒙特卡洛模拟算出的期权价值，图中BS为由BS方程算出的期权价值

  • 美式期权：

    注：图中行权代表将在此处美式期权会提前行权，该期权为四步二叉树，也可以为NN步(N>1)(N>1)

参考文献

1
2
[1]约翰·C·赫尔.期权、期货和其他衍生品:第9版[M].北京:清华大学出版社,2020.
[2]毛啸峰.期权定价数值方法的有效性分析[D].西南大学,2020.DOI:10.27684/d.cnki.gxndx.2020.001328.

附录

蒙特卡洛模拟原理

由蒙特卡洛算法的理论基础分析，蒙特卡洛算法是由随机变量XX的样本X1,X2,X3,...,XNX_1,X_2,X_3,...,X_N的算术平均值：

XN‾=1N∑i=1NXi\overline{X_N}=\frac{1}{N} \sum_{i=1}^N X_i

作为我们所求解的近似值。而X1,X2,X3,...,XNX_1,X_2,X_3,...,X_N独立同分布，且具有有限期望值(E(X)<∞\mathrm{E}(\mathrm{X})<\infty)。

由大数定律可知：

P(lim⁡N→∞XN‾=E(X))=1P\left(\lim _{N \rightarrow \infty} \overline{X_N}=E(X)\right)=1

即：随机变量XX的抽样样本均值XNX_N，当样本量NN足够大时，依概率收敛于它的期望值E(X)E(X)。

由伯努利大数定理，可以用k/nk/n作为蒙特卡洛模拟得到的概率pp的估计值，所以可将NN个随机变量的值g(x1),g(x2),…g(xN)g\left(x_1\right), g\left(x_2\right), \ldots g\left(x_N\right)的算术平均值：

gN^=1 N∑i=1Ng(xi)\widehat{\mathrm{g}_{\mathrm{N}}}=\frac{1}{\mathrm{~N}} \sum_{\mathrm{i}=1}^{\mathrm{N}} \mathrm{g}\left(\mathrm{x}_{\mathrm{i}}\right)

作为概率pp的估计值。

求解误差

考虑给定的置信度为1−α(0<α<1)1-\alpha(0<\alpha<1)，设估计精度为ϵ\epsilon，即：

P{∣p^−p∣<ε}=P{∣kn−p∣<ε}>1−a\mathrm{P}\{|\hat{\mathrm{p}}-\mathrm{p}|<\varepsilon\}=\mathrm{P}\left\{\left|\frac{\mathrm{k}}{\mathrm{n}}-\mathrm{p}\right|<\varepsilon\right\}>1-a

成立。

记nn次独立实验中AA出现的次数为knk_n，则kn∼B(n,p)\mathrm{k}_{\mathrm{n}} \sim \mathrm{B}(\mathrm{n}, \mathrm{p})，根据T−LT-L中心极限定理知：

P{∣p^−p∣<ε}=P{∣kn−p∣<ε}=P{−nεnp(1−p)<kn−npnp(1−p)<nεnp(1−p)}≈2ϕ(nεnp(1−p))−1\begin{array}{l} \mathrm{P}\{|\hat{\mathrm{p}}-\mathrm{p}|<\varepsilon \}\\ =\mathrm{P}\left\{ \left| \frac{\mathrm{k}}{\mathrm{n}}-\mathrm{p} \right|<\varepsilon \right\}\\ =\mathrm{P}\left\{ -\frac{\mathrm{n}\varepsilon}{\sqrt{\mathrm{np(}1-\mathrm{p)}}}<\frac{\mathrm{k}_{\mathrm{n}}-\mathrm{np}}{\sqrt{\mathrm{np(}1-\mathrm{p)}}}<\frac{\mathrm{n}\varepsilon}{\sqrt{\mathrm{np(}1-\mathrm{p)}}} \right\}\\ \approx 2\phi \left( \frac{\mathrm{n}\varepsilon}{\sqrt{\mathrm{np(}1-\mathrm{p)}}} \right) -1\\ \end{array}

令

2ϕ(nεnp⁡(1−p))−1>1−α2 \phi\left(\frac{\mathrm{n} \varepsilon}{\sqrt{\operatorname{np}(1-p)}}\right)-1>1-\alpha

即：

ϕ(nεnp(1−p))>1−α/2\phi\left(\frac{\mathrm{n} \varepsilon}{\sqrt{\mathrm{np}(1-\mathrm{p})}}\right)>1-\alpha/ 2

则标准正态分布的上侧分位数

u1−α/2=nε/np(1−p)\mathrm{u}_{1-\alpha/ 2}=\mathrm{n} \varepsilon / \sqrt{\mathrm{np}(1-\mathrm{p})}

解得：

n=p(1−p)ε2u1−α/22\mathrm{n}=\frac{\mathrm{p}(1-\mathrm{p})}{\varepsilon^2} \mathrm{u}_{1-\mathrm{\alpha} / 2}^2

由此可以看出，nn与ε2\varepsilon^2呈反比，即统计样本数量越大，误差ϵ\epsilon越小。

方差分析

若将误差ϵ\epsilon定义为:

ε=λaσ/N ( α 为置信度, N 为样本数量, σ 为标准差）\varepsilon=\lambda_a \sigma / \sqrt{N} \text { ( } \alpha \text { 为置信度, } N \text { 为样本数量, } \sigma \text { 为标准差）}

则σ\sigma越小，ε\varepsilon越小。（此处求得的误差ε\varepsilon为概率误差，且均方差σ\sigma是未知的)可以通过样本求得σ\sigma​的估计值

σ^=1N∑i=1NXi2−(1N∑i=1NXi)2\widehat{\sigma}=\sqrt{\frac{1}{N} \sum_{i=1}^N X_i{ }^2-\left(\frac{1}{N} \sum_{i=1}^N X_i\right)^2}

来代替σ\sigma。

  • 当实验不同次数后，可以得到不同实验次数NN对应的σ\sigma值：
  • 当NN很小(0-100)时，σ\sigma的值偏差极大。